Leetcode 129 - Sum Root to Leaf Numbers

Problem Description

Leetcode 129 - Sum Root to Leaf Numbers

You are given the root of a binary tree containing digits from 0 to 9 only.

Each root-to-leaf path in the tree represents a number.

• For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.

Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.

A leaf node is a node with no children.

Examples

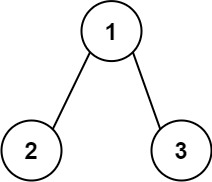Input: root = [1,2,3]

Output: 25

Explanation:

• The root-to-leaf path 1->2 represents the number 12.
• The root-to-leaf path 1->3 represents the number 13.

Therefore, sum = 12 + 13 = 25.

Thought Process / Intuition

My thought process when I see a binary tree is to either employ DFS or BFS, like instinctively. As the problem requires us to find the total sum of ALL root to leaf numbers, we use DFS to traverse the entire tree. As we traverse the tree, we keep track of a path, like shown in the example 1 -> 2 -> 3 as a list, then we convert it into a number and add it to the total sum. We repeat this process for all root to leaf paths and return the total sum.

Approach

1. We define a helper function dfs that takes the current node and the path to the current node.
2. If the current node is a leaf node, we convert the path to an integer and append it to the result list.
3. If the current node is not a leaf node, we recursively call the dfs function on the left and right children of the current node.
4. We initialize an empty list res to store the results and call the dfs function on the root node with an initial path of the root node's value.
5. Finally, we return the sum of all the numbers in the res list.

Solution

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sumNumbers(self, root: Optional[TreeNode]) -> int:
        def dfs(root, path):
            if root.left is None and root.right is None:
                res.append(int(''.join(path)))
                return
            for child in [root.left, root.right]:
                if child is None:
                    continue
                path.append(str(child.val))
                dfs(child, path)
                path.pop()
                
                
        res = []
        dfs(root, [str(root.val)])
        return sum(res)

Complexity Analysis

Time complexity: $O(n)$

• The function operates in $O(n)$ time, where n is the number of nodes in the binary tree. This is because each node needs to be visited once to determine if it's a left leaf node or not.

Space complexity: $O(n)$

• The space complexity is $O(h)$, where h represents the height of the binary tree. This accounts for the space used by the recursive call stack.

• In the worst-case scenario of a completely unbalanced tree, where the height equals the number of nodes $(n)$, the space complexity becomes $O(n)$.

• Conversely, in the best-case scenario of a balanced tree, where the height is logarithmic $(log(n))$, the space complexity is reduced to $O(log(n))$.

• However, in my solution, since I keep converting to strings, I actually create $O(n)$ strings. So the space complexity is $O(n)$.