Leetcode 1325 - Delete Leaves with a Given Value

Problem Description

Given a binary tree root and an integer target, delete all the leaf nodes with value target.

Note that once you delete a leaf node with value target, if its parent node becomes a leaf node and has the value target, it should also be deleted (you need to continue doing that until you cannot).

Examples

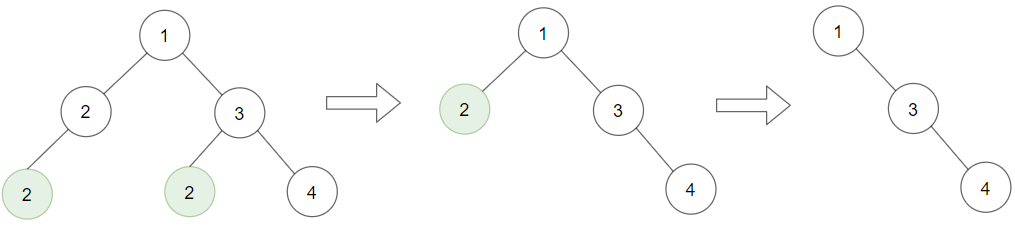
Input: root = [1,2,3,2,null,2,4], target = 2

Output: [1,null,3,null,4]

Explanation: Leaf nodes in green with value target = 2 are removed (Picture in left). After removing, new nodes become leaf nodes with value target = 2 (Picture in center).

Thought Process / Intuition

Binary tree question that wants us to return a modified tree with targeted nodes removed. First instinct should be to use DFS, and the only challenge is to ensure that removing a leaf node might cause a non-leaf node to become a leaf node itself, so you have to put the leaf node check after the recursive call. Otherwise if you didn't, you can still solve brute force which is my first attempt by hard coding the constraints to run dfs 3000 times.

Approach

1. Create a dfs function that takes in a node, root.
2. Check if the node is None.
3. Run the dfs recursive calls on the left and right children FIRST
4. Check if the node is a leaf node, and remove if its value is equal to the target.(Important to place this code after the recursive call as we want to preserve the check for the parent nodes as well.)
5. Return the root.

Solution

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def removeLeafNodes(self, root: Optional[TreeNode], target: int) -> Optional[TreeNode]:
        def dfs(root):
            if root is None:
                return root
            root.left = dfs(root.left)
            root.right = dfs(root.right)
            if root.left is None and root.right is None:
                if root.val == target:
                    return None
                return root
            return root
        return dfs(root)

Complexity Analysis

Time complexity: $O(n)$

• The function operates in $O(n)$ time, where n is the number of nodes in the binary tree.
• The function's time complexity is proportional to the number of nodes traversed. At each node visit, operations are performed at $O(1)$ time, such as checking if the node is a leaf node and removing it if it matches the target value.
• Therefore, the time complexity is $O(n)$.

Space complexity: $O(n)$

• The space complexity is $O(h)$, where h represents the height of the binary tree. This accounts for the space used by the recursive call stack.
• In the worst-case scenario of a completely unbalanced tree, where the height equals the number of nodes $(n)$, the space complexity becomes $O(n)$.
• Conversely, in the best-case scenario of a balanced tree, where the height is logarithmic $(log(n))$, the space complexity is reduced to $O(log(n))$.
• Theres an additional space usage for the path list which is $O(h)$. However, since we pop the path list after each dfs, the list does not grow with $n$. Thus, the dominant space complexity is still the height of the recursion stack which is $O(h)$.
• In the worst-case, the space complexity is $O(n)$.

Shoutout to My Friends' Solutions

My Solution