Problem Description
There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [, ] denotes a bi-directional edge between vertex and vertex . Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
You want to determine if there is a valid path that exists from vertex source to vertex destination.
Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.
Examples
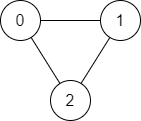
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2
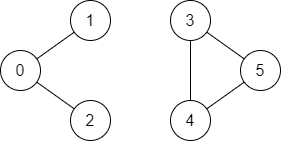
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Thought Process / Intuition
When reading the problem, it is pretty obvious that its a union find problem, as we want to return a boolean value whether there is a path from source to destination, which we can reduce to a union find problem of trying to find if two nodes are in the same union find. The edges allows us to easily construct our union find data structure.
Approach
- Create a UnionFind class with the following methods:
__init__: Initialize theiddictionary to store the parent of each vertex.find: Find the parent of a vertex and perform path compression.union: Perform a union operation between two vertices.
- Create an instance of the UnionFind class.
- Iterate through the edges and perform union operations.
- Check if the source and destination vertices are in the same union find set.
Solution
class UnionFind:
def __init__(self):
self.id = {}
def find(self, x):
y = self.id.get(x, x)
if y != x:
self.id[x] = y = self.find(y)
return y
def union(self, x, y):
self.id[self.find(x)] = self.find(y)
class Solution:
def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
uf = UnionFind()
for edge in edges:
uf.union(edge[0], edge[1])
return uf.find(source) == uf.find(destination)Complexity Analysis
Time complexity:
- This solution's time complexity is dependent on the number of Union-Find operations. As we iterate through the edges and perform union operations, the time complexity is , where represents the number of edges and is the number of vertices. As my union find data structure only uses path compression, the amortized time complexity is for each union-find operation. If we used union by rank on top of path compression, the amortized time complexity can be shortened to for each union-find operation.
Space complexity:
- The space complexity of this solution is , where represents the number of vertices in the graph. The Union-Find data structure uses a dictionary to store the parent of each vertex, resulting in a space complexity of .