Leetcode 1992 - Find All Groups of Farmland

Problem Description

You are given a 0-indexed m x n binary matrix land where a 0 represents a hectare of forested land and a 1 represents a hectare of farmland.

To keep the land organized, there are designated rectangular areas of hectares that consist entirely of farmland. These rectangular areas are called groups. No two groups are adjacent, meaning farmland in one group is not four-directionally adjacent to another farmland in a different group.

land can be represented by a coordinate system where the top left corner of land is (0, 0) and the bottom right corner of land is (m-1, n-1). Find the coordinates of the top left and bottom right corner of each group of farmland. A group of farmland with a top left corner at (r1, c1) and a bottom right corner at (r2, c2) is represented by the 4-length array [r1, c1, r2, c2].

Return a 2D array containing the 4-length arrays described above for each group of farmland in land. If there are no groups of farmland, return an empty array. You may return the answer in any order.

Examples

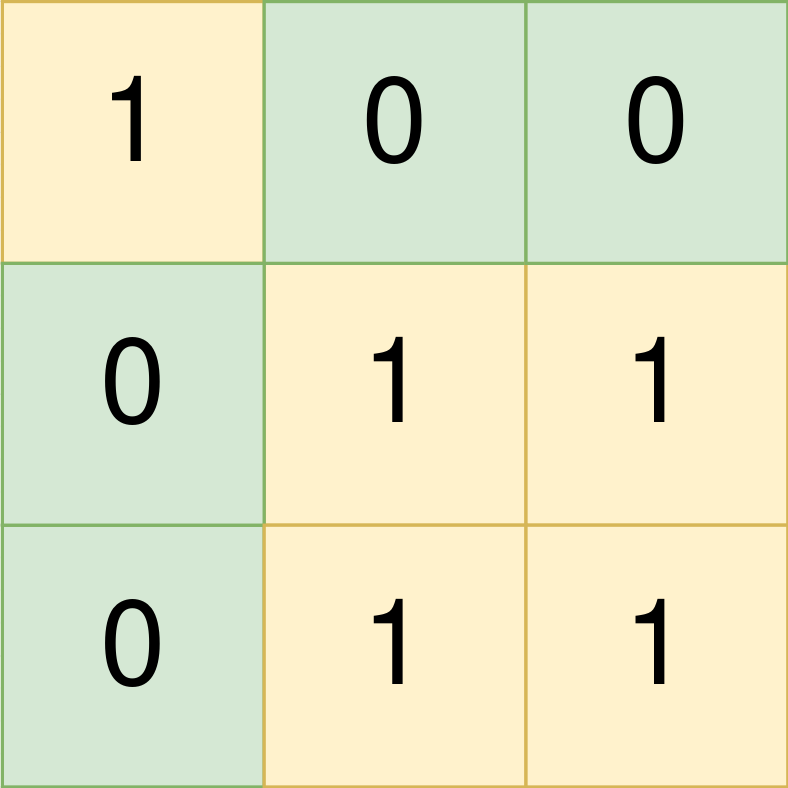
Input: land = [[1,0,0],[0,1,1],[0,1,1]]

Output: [[0,0,0,0],[1,1,2,2]]

Explanation:

• The first group has a top left corner at land[0][0] and a bottom right corner at land[0][0].
• The second group has a top left corner at land[1][1] and a bottom right corner at land[2][2].

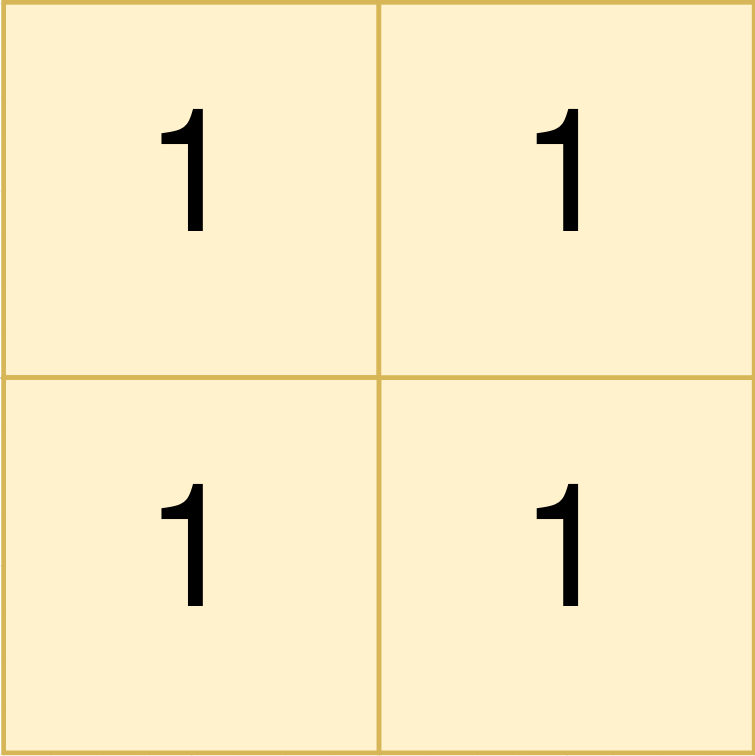
Input: land = [[1,1],[1,1]]

Output: [[0,0,1,1]]

Explanation: The first group has a top left corner at land[0][0] and a bottom right corner at land[1][1].

Input: land = [[0]]

Output: []

Explanation: There are no groups of farmland.

Thought Process / Intuition

The problem is asking us to find the coordinates of the top left and bottom right corner of each group of farmland in the given binary matrix land. We can achieve this by iterating through the matrix and finding the farmland groups by traversing row wise and column wise once we find a land cell that is part of a farmland group. Then, we can update the farmland cells to 0 to avoid counting them again.

Approach

1. Initialize an empty list farmlands to store the coordinates of the top left and bottom right corner of each farmland group.
2. Iterate through each cell in the matrix land (outer loop).
3. If the current cell is a farmland cell and is not part of an existing farmland group, we start two while loops (inner loops), one for the rows and one for the columns, to find the coordinates for the bottom right corner of the farmland group.
4. Update the farmland cells to 0 to avoid counting them again.
5. Append the coordinates of the farmland group to the farmlands list.
6. Return the list of farmland groups.

Solution

from typing import List

class Solution:
    def findFarmland(self, land: List[List[int]]) -> List[List[int]]:
        num_rows, num_columns = len(land), len(land[0])
      
        farmlands = []

        for row in range(num_rows):
            for col in range(num_columns):
                if (land[row][col] == 0 or
                   (col > 0 and land[row][col - 1] == 1) or
                   (row > 0 and land[row - 1][col] == 1)):
                    continue

                farmland_end_row, farmland_end_col = row, col

                while farmland_end_row + 1 < num_rows and land[farmland_end_row + 1][col] == 1:
                    farmland_end_row += 1

                while farmland_end_col + 1 < num_columns and land[farmland_end_row][farmland_end_col + 1] == 1:
                    farmland_end_col += 1

                farmlands.append([row, col, farmland_end_row, farmland_end_col])
              
                for i in range(row, farmland_end_row + 1):
                    for j in range(col, farmland_end_col + 1):
                        land[i][j] = 0
                      
        return farmlands

Complexity Analysis

Time complexity: $O(m * n)$

• The time complexity of this solution is $O(m * n)$, where $m$ represents the number of rows and $n$ represents the number of columns in the input matrix land. We iterate through each cell in the matrix, and for each cell, we traverse the rows and columns to find the farmland group.
• Each cell is visited at most twice, once when we check if it is part of a farmland group and once when we update the cell to 0 after finding the farmland group. Therefore, the time complexity is $O(m * n)$.

Space complexity: $O(1)$

• The space complexity of the solution is $O(1)$, as we are not using any additional data structures that grow with the input size. We are updating the input matrix land in place to mark the farmland groups, and the output array farmlands only contains the coordinates of the farmland groups.

Shoutout to My Friends' Solutions

Kurt's Solution

Si Yuan's Solution