Leetcode 310 - Minimum Height Trees

Problem Description

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Examples

Example 1:

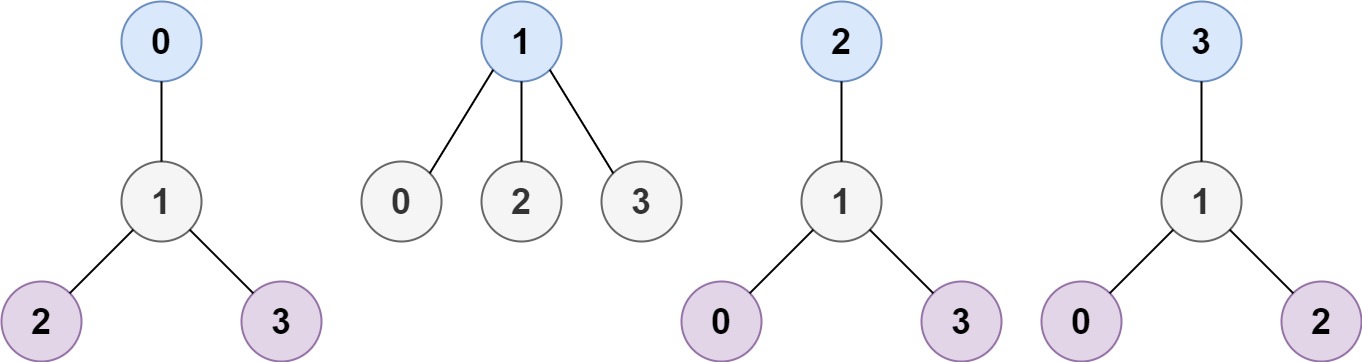
Leetcode 310 Example 1

Input: n = 4, edges = [[1,0],[1,2],[1,3]]

Output: [1]

Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

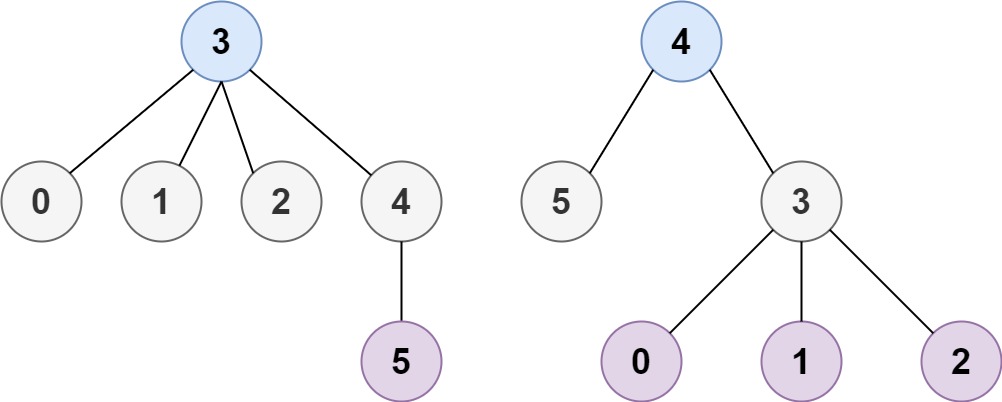
Leetcode 310 Example 2

Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]

Output: [3,4]

Constraints:

$1` < = n < = 2 * 10^4$
edges.length == n - 1
$0 < = a_i, b_i < n$
$a_i != b_i$ All the pairs $(a_i, b_i)$ are distinct. The given input is guaranteed to be a tree and there will be no repeated edges.

Thought Process / Intuition

My initial idea was to use BFS on every single node and return the nodes that had the shortest height. However, this would be inefficient as we would have to traverse the entire tree for every node. The time complexity would be $O(V * E)$ , where $V$ is the number of vertices and $E$ is the number of edges. This is not efficient, and times out on leetcode, as $V = E = 2 * 10^4$ . According to Algomonster, the maximum no. of operations before timeout is around $10^7$ . So, we need to optimize our solution. Admittedly, I could not solve the question, so I referred to Algomonster's solution.

Approach

We first handle the base case where if there is only one node, we return it as the centroid.
We initialize a graph and a degree list to store the degree of each node.
We build the graph and keep track of each node's degree.
We initialize a queue with all leaf nodes (nodes with degree 1).
We keep trimming leaves until the centroid/s is/are found.
We return the final centroids of the tree, which will have the minimum height.

Initial Solution

from collections import deque
class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        def bfs(root):
            nonlocal max_so_far
            nonlocal res
            queue = deque([root])
            count = -1
            visited = set()
            while len(queue) > 0:
                if count > max_so_far:
                    break
                n = len(queue)
                for _ in range(n):
                    node = queue.popleft()
                    for edge in edges:
                        if node not in visited and node in edge:
                            if node == edge[0]:
                                if edge[1] not in visited:
                                    queue.append(edge[1])
                            else:
                                if edge[0] not in visited:
                                    queue.append(edge[0])
                    visited.add(node)
                count += 1
            if count > max_so_far:
                return
            if count < max_so_far:
                max_so_far = count
                res = []
            res.append(root)
        res = []
        max_so_far = 2 * 10**4
        for node in range(n):
            bfs(node)
        return res

Optimized Solution, credit Algomonster

from collections import defaultdict, deque
class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if n == 1:
            return [0]
        graph = defaultdict(list)
        degree = [0] * n

        for node1, node2 in edges:
            graph[node1].append(node2)
            graph[node2].append(node1)
            degree[node1] += 1
            degree[node2] += 1
      
        leaves_queue = deque(i for i in range(n) if degree[i] == 1)
        min_height_trees = []
      
        while leaves_queue:
            min_height_trees.clear()
            for _ in range(len(leaves_queue)):
                current_node = leaves_queue.popleft()
                min_height_trees.append(current_node)
                for neighbor in graph[current_node]:
                    degree[neighbor] -= 1
                    if degree[neighbor] == 1:
                        leaves_queue.append(neighbor)
      
        return min_height_trees

Complexity Analysis

Time complexity: $O(V + E)$

The time complexity of this solution is $O(V + E)$ , where $V$ is the number of vertices and $E$ is the number of edges in the graph.
Constructing the graph takes $O(V + E)$ time, since we go through all edges and insert both the edge connections into the graph representation.
Initializing the degree array takes $O(V)$ time.
Initializing the queue q with all leaves takes $O(V)$ time in the worst case (when all nodes are leaves, except one or two).
The while loop processes each node once when it becomes a leaf, decrementing the degrees and potentially adding new leaves to the queue. Every edge is looked at exactly twice (once for each vertex it connects) over the entire runtime of the algorithm. So the complexity associated with this part is $O(E)$ .
Therefore, the loop and ensuing operations are bounded by the total number of edges, making the overall time complexity $O(V + E)$ as, in graph algorithms, we commonly take the sum of vertices and edge processing times.

Space complexity: $O(V + E)$

The space complexity of this solution is $O(V + E)$ .
The graph dictionary takes $O(E)$ space.
The degree array takes $O(V)$ space.
The leaves_queue can take up to $O(V)$ space in the worst case.
The answer array can take up to $O(V)$ space in the worst case.
Therefore, the overall space complexity is $O(V + E)$ .

Shoutout to My Friends' Solutions

Kurt's Solution

Si Yuan's Solution