Leetcode 404 - Sum of Left Leaves

Problem Description

Given the root of a binary tree, return the sum of all left leaves.

Example

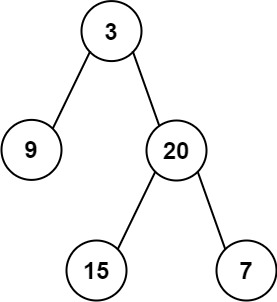
Input: root = [3,9,20,null,null,15,7]

Output: 24

Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.

Thought Process / Intuition

Yeah so when I first saw this question, straight away I recognised it as DFS, as we want to traverse every node and add the value of the left leaf node to a total. As such, we can just use DFS on trees to solve this problem, and it should be pretty straightforward.

What was abit tricky was to figure out the code to identify the left leaf nodes. To do so, you had to check if the current node had a left child, and then check if that left child is a leaf node, which is child.left is None and child.right is None.

Approach

This recursive solution, employing Depth-First Search (DFS), efficiently sums up the values of all left leaves in a binary tree. Here's how it works:

Base Case:

• If the current node is None (indicating a leaf node), return 0, as there's no contribution from non-existent leaves.

Identifying Left Leaves:

• For each left child node, check if it's a leaf by ensuring both its children are None.
• If it's a left leaf, add its value to the running total 'res'.

Recursive Calls:

Recur on the left child to find left leaves in its subtree. Recur on the right child to explore potential left leaves, though these won't contribute directly to the sum unless they have left leaves in their subtrees.

Returning the Result:

Sum up values from left leaves found in both left and right subtrees. Return the final sum 'res', representing the total sum of left leaves in the tree. This approach ensures each node is visited once, identifying and summing left leaves effectively. With a time complexity of O(n) and space complexity of O(h) (where n is the number of nodes and h is the height of the tree), the solution is both efficient and elegant. The critical part of the code involves checking for left leaves and making recursive calls to traverse the tree.

Solution

class Solution:
    def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
        def dfs(root):
            if root is None:
                return 0
            total = 0
            if root.left and root.left.left is None and root.left.right is None:
                total += root.left.val
            total += dfs(root.left)
            total += dfs(root.right)
            return total
        return dfs(root)

Complexity Analysis

Time complexity: $O(n)$

• The function operates in $O(n)$ time, where n is the number of nodes in the binary tree. This is because each node needs to be visited once to determine if it's a left leaf node or not.

Space complexity: $O(n)$

• The space complexity is $O(h)$, where h represents the height of the binary tree. This accounts for the space used by the recursive call stack.
• In the worst-case scenario of a completely unbalanced tree, where the height equals the number of nodes $(n)$, the space complexity becomes $O(n)$.
• Conversely, in the best-case scenario of a balanced tree, where the height is logarithmic $(log(n))$, the space complexity is reduced to $O(log(n))$.