Leetcode 623 - Add One Row to Tree

Problem Description

Given the root of a binary tree and two integers val and depth, add a row of nodes with value val at the given depth depth.

Note that the root node is at depth 1.

The adding rule is:

• Given the integer depth, for each not null tree node cur at the depth depth - 1, create two tree nodes with value val as cur's left subtree root and right subtree root.

• cur's original left subtree should be the left subtree of the new left subtree root.

• cur's original right subtree should be the right subtree of the new right subtree root.

• If depth == 1 that means there is no depth depth - 1 at all, then create a tree node with value val as the new root of the whole original tree, and the original tree is the new root's left subtree.

Examples

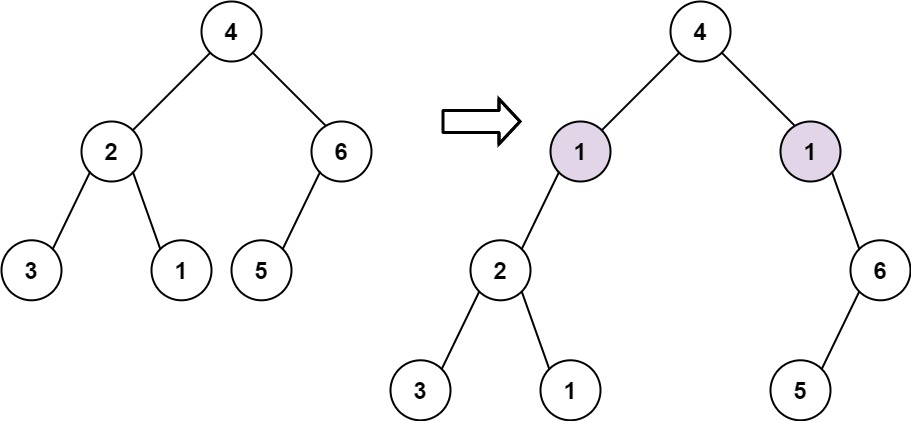
Input: root = [4,2,6,3,1,5], val = 1, depth = 2

Output: [4,1,1,2,null,null,6,3,1,5]

Thought Process / Intuition

Once again, like yesterday, we have a tree problem. This time, we have to add a row of nodes at a certain depth. The problem is a bit more complex than yesterday's, but the approach is still the same.

I think both DFS and BFS would be able to work, but I decided to use DFS. The idea is to traverse the tree and when we reach the depth - 1, we add the new nodes.

Approach

1. Create a dfs function that takes in the root and the current depth.
2. If the current depth is equal to the target depth - 1, add the new nodes.
3. Then recursively call the dfs function on the left and right children of the current node.
4. Finally, I return the root of the tree.

Initial Attempt

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def addOneRow(self, root: Optional[TreeNode], val: int, depth: int) -> Optional[TreeNode]:
        if depth == 1:
            new_node = TreeNode(val, root, None)
            return new_node
        def dfs(root, start_index):
            if root is None:
                return
            temp1 = root.left
            temp2 = root.right
            if start_index == depth:
                root.left = TreeNode(val)
                root.right = TreeNode(val)
            for child in [temp1, temp2]:
                if child and child == temp1 and start_index == depth:
                    new_node = TreeNode(val, child, None)
                    root.left = new_node
                if child and child == temp2 and start_index == depth:
                    new_node = TreeNode(val, None, child)
                    root.right = new_node
                dfs(child, start_index + 1)
        dfs(root, 2)
        return root

Modified Solution

Kurt's Solution

• After looking through Kurt's solution, I realised my code was very complex and could be solved more beautifully with recursion.

class Solution:
    def addOneRow(self, root: Optional[TreeNode], val: int, depth: int):
        if depth == 1:
            new_node = TreeNode(val, root, None)
            return new_node
        def dfs(root, start_index):
            if root is None:
                return
            if start_index == depth - 1:
                root.left = TreeNode(val, left=root.left, right=None)
                root.right = TreeNode(val, left=None, right=root.right)
            dfs(root.left, start_index + 1)
            dfs(root.right, start_index + 1)
        dfs(root, 1)
        return root

Complexity Analysis

Time complexity: $O(n)$

• The function operates in $O(n)$ time, where n is the number of nodes in the binary tree.
• The function's time complexity is proportional to the number of nodes traversed. However, as we can terminate at a certain depth, the number of nodes traversed could actually be less than n.
• However, we care about the worst case. In the worst case, we would have to traverse all the nodes in the tree if the depth is at the maximum depth of the tree.
• Therefore, the time complexity is $O(n)$.

Space complexity: $O(h)$

• The space complexity is $O(h)$, where h represents the height of the binary tree. This accounts for the space used by the recursive call stack.
• In the worst-case scenario of a completely unbalanced tree, where the height equals the number of nodes $(n)$, the space complexity becomes $O(n)$.
• Conversely, in the best-case scenario of a balanced tree, where the height is logarithmic $(log(n))$, the space complexity is reduced to $O(log(n))$.