Leetcode 988 - Smallest String Starting From Leaf

Problem Description

You are given the root of a binary tree where each node has a value in the range [0, 25] representing the letters 'a' to 'z'.

Return the lexicographically smallest string that starts at a leaf of this tree and ends at the root.

As a reminder, any shorter prefix of a string is lexicographically smaller.

• For example, "ab" is lexicographically smaller than "aba".

A leaf of a node is a node that has no children.

Examples

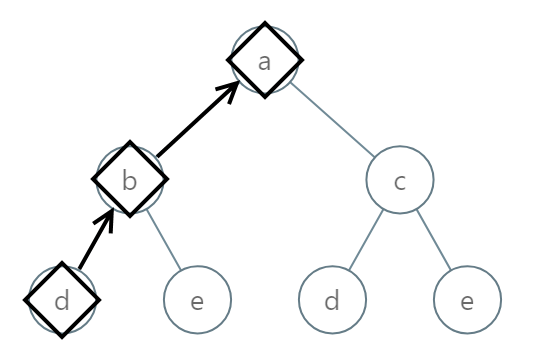
Input: root = [0,1,2,3,4,3,4]

Output: "dba"

Input: root = [25,1,3,1,3,0,2]

Output: "adz"

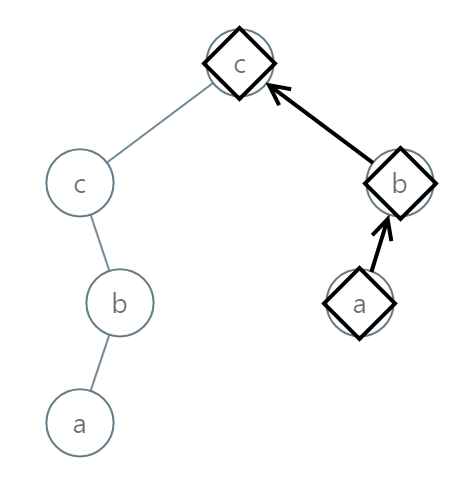
Input: root = [2,2,1,null,1,0,null,0]

Output: "abc"

Thought Process / Intuition

Binary Tree problem, again! This time, we have to find the lexicographically smallest string that starts at a leaf and ends at the root.

As always, the thught process should be to use DFS or BFS. Finding a string that starts at a leaf and ends at the root means we need to keep track of the path, so we should use backtracking and DFS.

Since we want a path from leaf to the root, my first idea was to use a queue and insert the next item in the path on the left of the queue to return the final path. However, I realised we can just use a normal list and keep track of the path, and just reverse the list at the end. Both methods work to keep track of the path.

When adding the element into the path, as the value in the nodes are integers, we need to convert it into a string. My first attempt actually had me create a mapping list where each index corresponded to the character, i.e. mapping = ['a', 'b', 'c', ..., 'z'].

However, a friend of mine walked past and casually dropped the hint that I could just use the chr(97 +) function to convert the integer to a character, as 97 was the ASCII value for 'a'.

Now that we have all the paths, we just append it to our final result list, and we can either sort the list and return the first item or use the min() function to return the lexicographically smallest string.

Approach

1. Create a dfs function that takes in the root and the current depth.
2. If the current depth is equal to the target depth - 1, add the new nodes.
3. Then recursively call the dfs function on the left and right children of the current node.
4. Finally, I return the root of the tree.

Solution

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def smallestFromLeaf(self, root: Optional[TreeNode]) -> str:
        def dfs(root, path):
            if root is None:
                return
            if root.left is None and root.right is None:
                path.appendleft(chr(97 + root.val))
                res.append(''.join(path))
                path.popleft()
                return
            for child in [root.left, root.right]:
                path.appendleft(chr(97 + root.val))
                dfs(child, path)
                path.popleft()
        res = []
        path = deque([])
        dfs(root, path)
        return min(res)

Alternate Solution

Without using a queue, we can just use a list to keep track of the path and reverse it at the end. (Beats 90% Time and 50% space)

class Solution:
    def smallestFromLeaf(self, root: Optional[TreeNode]) -> str:
        def dfs(root, path):
            if root is None:
                return
            if root.left is None and root.right is None:
                path.append(chr(97 + root.val))
                res.append(''.join(path[::-1]))
                path.pop()
                return
            for child in [root.left, root.right]:
                path.append(chr(97 + root.val))
                dfs(child, path)
                path.pop()
        res = []
        path = []
        dfs(root, path)
        return min(res)

Alternate Solution 2

The most optimum solution in terms of space and time complexity. This was provided by Taufiq when he casually strolled past. The idea is that you can keep track of the smallest string during the whole dfs and just update it and return it at the end. (Beats 99% Space and 90% Time)

class Solution:
    def smallestFromLeaf(self, root: Optional[TreeNode]) -> str:
        smallest_string = 'z'*8500
        def dfs(node, path):
            nonlocal smallest_string
            if node:
                path.append(chr(97 + node.val))
                if node.left is None and node.right is None:
                    current_string = ''.join(path[::-1])
                    smallest_string = min(smallest_string, current_string)
                dfs(node.left, path)
                dfs(node.right, path)
                path.pop()
        dfs(root, [])
        return smallest_string

Complexity Analysis

Time complexity: $O(n)$

• The function operates in $O(n)$ time, where n is the number of nodes in the binary tree.
• The function's time complexity is proportional to the number of nodes traversed. At each node visit, operations are performed at $O(1)$ time, such as appending and popping from the path list.
• The min() function at the end is upper bounded $O(n)$, but in actuality is a lot lesser as the number of paths is less than the number of nodes.
• Therefore, the time complexity is $O(n)$.

Space complexity: $O(h)$

• The space complexity is $O(h)$, where h represents the height of the binary tree. This accounts for the space used by the recursive call stack.
• In the worst-case scenario of a completely unbalanced tree, where the height equals the number of nodes $(n)$, the space complexity becomes $O(n)$.
• Conversely, in the best-case scenario of a balanced tree, where the height is logarithmic $(log(n))$, the space complexity is reduced to $O(log(n))$.
• Theres an additional space usage for the path list which is $O(h)$. However, since we pop the path list after each dfs, the list does not grow with $n$. Thus, the dominant space complexity is still the height of the recursion stack which is $O(h)$.

Shoutout to My Friends' Solutions

Kurt's Solution

Si Yuan's Solution